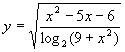|
|
Тема:
«Логарифмическая функция». |
||||||||||||||||||||||||||||||||||
|
Основная цель: познакомить учащихся логарифмической
функцией и ее свойствами, научить решать логарифмические уравнения и
неравенства, системы, содержащие логарифмические уравнения. |
|||||||||||||||||||||||||||||||||||
|
Задачи: изучение программного материала дает
учащимся возможность: ü
систематизировать
и развивать знания о функции как важнейшей математической модели; ü
овладеть
свойствами логарифмической функции, уметь строить ее график, развивать
графическую культуру, применять приемы преобразования графиков; ü
овладеть
техникой решения уравнений и неравенств. |
|||||||||||||||||||||||||||||||||||
|
Уровень обязательной подготовки определяется следующими
требованиями: ü
определять
значение функции по значению аргумента; ü
уметь строить
график функции вида у=logax (a>0, a ü
уметь
применять вычислительную технику для нахождения значений логарифмов чисел; ü
решать простейшие
логарифмические уравнения и неравенства; ü
иметь
представление о графическом методе решения уравнений и неравенств. |
|||||||||||||||||||||||||||||||||||
|
Обязательным является умение выполнять задания следующего
типа: №1 на рисунке изображен график функции у=
у=
0 1 х №2 Какие из чисел -1; 0; 1; 2; 4; 8 являются корнями уравнения №3 Решить уравнения: а) г) №4 Решить неравенства: а) №5 Найдите область определения функции: у= №6 Сравните числа: №7 Определить число корней уравнения:: |
|||||||||||||||||||||||||||||||||||
|
Поурочное
планирование темы: «Логарифмическая функция». 19
часов (Учебник Ш.А.Алимов и др.)
|
|||||||||||||||||||||||||||||||||||
|
I.
Тест на
определение истинности (ложности) утверждения. 1) lg
0.001=-3; 2) II. Тест с
выбором ответа. |
|||||||||||||||||||||||||||||||||||
|
А) Найти значение выражения: 1. 2. 3. 4. 5. 3 6. |
Б) Найти х: 1. А) 14,
В) 21, С) 90; D) 290. 2. А) 1, В) 3, С) 13; D) 313. 3. А) 19, В) 27, С) 3; D) 53. 4. А) 4, В) 5. А) 4, В) 5, С) 3; D) 6. |
||||||||||||||||||||||||||||||||||
|
«Определение логарифма. Свойства логарифмов». 1 карточка 1)
Дать определение
логарифма. Записать основное логарифмическое тождество. 2)
Подставить
недостающие числа: log ð16=4; log24=ð; log4ð=2 3)
Вычислить: А) 4)
Решить
уравнения: А)2х=5; Б) 42х+3=6; В)72х+7х-12=0 2 карточка 1)
Сформулировать и
записать свойства логарифмов. 2)
Сравните: 3lg2 и 2lg3. 3)
Вычислите: а) lg2+lg5; б ) 4)
Решить
уравнения: а) 3 карточка 1)
Дать определение
десятичного и натурального логарифма. 2)
Вычислите на
калькуляторе lg6 и ln2. 3)
Вычислите: а) 4)
Решить
уравнения: а) 4 карточка 1)
Формула перехода
от одного основания логарифмов к другому. 2)
Вычислить: а) 3)
Решить
уравнения: а)logx4=2; б) 5 карточка 1)
Какие задачи
решаются с помощью логарифмов? 2)
При каких
значениях х имеет смысл выражение а) log3(12-x); б) log6(49-x2); в) log6 3)
Докажите 4)
Решить
уравнения: а) |
|||||||||||||||||||||||||||||||||||
|
«Логарифм.
Основные свойства. График логарифмической функции. Решение логарифмических
уравнений и неравенств». |
|||||||||||||||||||||||||||||||||||
|
1 вариант 1°.
Вычислите: а) 2°.
Определите n, если log2 n =6 3°.
Найти область определения функции y=log2
(x+1)-log3
(x-2). 4°. Изобразите
схематически график функции и запишите её свойства y=log7 x 5°.
Расположите числа в порядке возрастания:
6°.
Сравните числа: 7°.
Определите знак числа 8°.
Решите уравнение: 9. Решите неравенство: 10. Найдите D(y): 11. Решите уравнение: |
2 вариант 1°.
Вычислите: а) 2°.
Определите n, если log4 n = 3°.
Найти область определения функции y=lg (x2+2x-15). 4°.
Изобразите схематически график функции и запишите её свойства y=log0,2 x 5°.
Расположите числа в порядке возрастания:
6°.
Сравните числа: 7°.
Определите знак числа 8°.
Решите уравнение: 9. Решите неравенство: 10. Найдите D(y): 11. Решите уравнение: |
||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||



 .
.